Latest Posts
HDHub4u: Get Free HD Bollywood and Hollywood Movies
Hi Users! If you're passionate about films and constantly searching for new releases, then HDHub4u is your ultimate destination. Catering to movie buffs, this site...
How to Get Picasso App and Watch OTT Movies & Shows
Hi Peoples! Have you noticed that as digital entertainment evolves, it's becoming an essential part of our daily routines? The growth in technology has opened...
Wyll Meaning: The Interesting History Behind The Term
The Fascinating Origin of the Term "Wyll Meaning" Hi Proples! Have you stumbled upon the term "Wyll Meaning" and pondered its roots and importance? This...
Monday.com Login: Simple Guide to Getting into Your Account
In today's fast-paced corporate climate, competent project management tools are critical. Monday.com distinguishes out as a flexible and user-friendly tool for teams looking to optimize...
Yt.be Activate: Enjoy Watching YouTube on Your Smart TV
In the age of digital streaming, the melding of amusement and tech has spawned innovative platforms transforming our media consumption habits. Yt.be Activate stands out,...
Blooket.com: How Does Blooket Join and Play Works?
There are now a plethora of engaging and educational online games for students. Kahoot, Gimkit, SplashLearn, Quizlet, and many others are just a few examples....
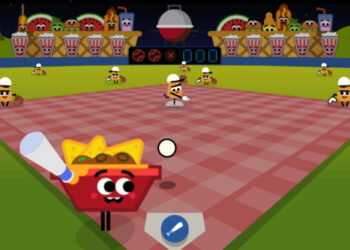
Google Baseball Unblocked: Discover the World of Baseball
Greetings, amazing followers! Prepare yourselves and gear up for an exciting dive into the world of Google Baseball Unblocked! This blog post welcomes you to...
What is Classwork.cc? Access Unblocked Games at School
Greetings, my esteemed audience! Today's subject is the online platform Classwork.cc and the nuanced discussion on how it's accessible without restrictions. For those in search...
HOW CAN MECHANICAL DESIGN SOFTWARE STREAMLINE PRODUCT DEVELOPMENT?
Mechanical design software stands as a beacon of innovation, offering a plethora of tools and functionalities that can significantly streamline the product development process. Dassault...
Proxiyum: Your Partner in Protecting Online Privacy
In today's technologically advanced era, where our actions are monitored and information is perpetually gathered, maintaining internet confidentiality has become incredibly important. Proxiyum, an intelligent...
How to Block Someone on TikTok Without Their Knowledge?
Let's go into how to block someone on TikTok so that your account stays positive and secure for you and your followers. In 2024, TikTok...
15 Top TikTok Video Downloader Apps To Try
TikTok Video Downloader Apps To Try: There are reportedly 1 billion users of TikTok each month. You might watch something intriguing today but won't be...
The Battle of Virtual Coins: Can Ethereum Surpass Bitcoin in 2024?
Since its launch in 2015, Ethereum has become a rising star and a popular currency in the crypto world. It presents game-changing potential with the...
Snokido is a Platform For Free Online Gaming
A popular online platform where a variety of games can be played is known as Snokido The website is compatible with a range of devices including...
RedGIFs Not Working, How To Fix? (Complete Guide)
Since the rise of social media and its increasing popularity. GIFs are quite useful in conveying emotions to others. GIFs may also be classified by...